Recently, I spent just over two years working in New Zealand (my native country), and was impressed by the number and quality of research projects in the field of mathematical biology and bioengineering. In some ways, researchers in the United States, myself included, are an insular group, unaware of much work that is going on in other countries. This is indeed a shame, as many countries offer unique opportunities to the mathematical biologist. For instance, pest control is of vital importance to the New Zealand economy, and mathematical models can, and have already, played a vital role in the development of control strategies. Similarly, New Zealand has a large number of endangered species, so models of species preservation have an important role to play, while the unusual flora and fauna offer unique opportunities to the evolutionary biologist.

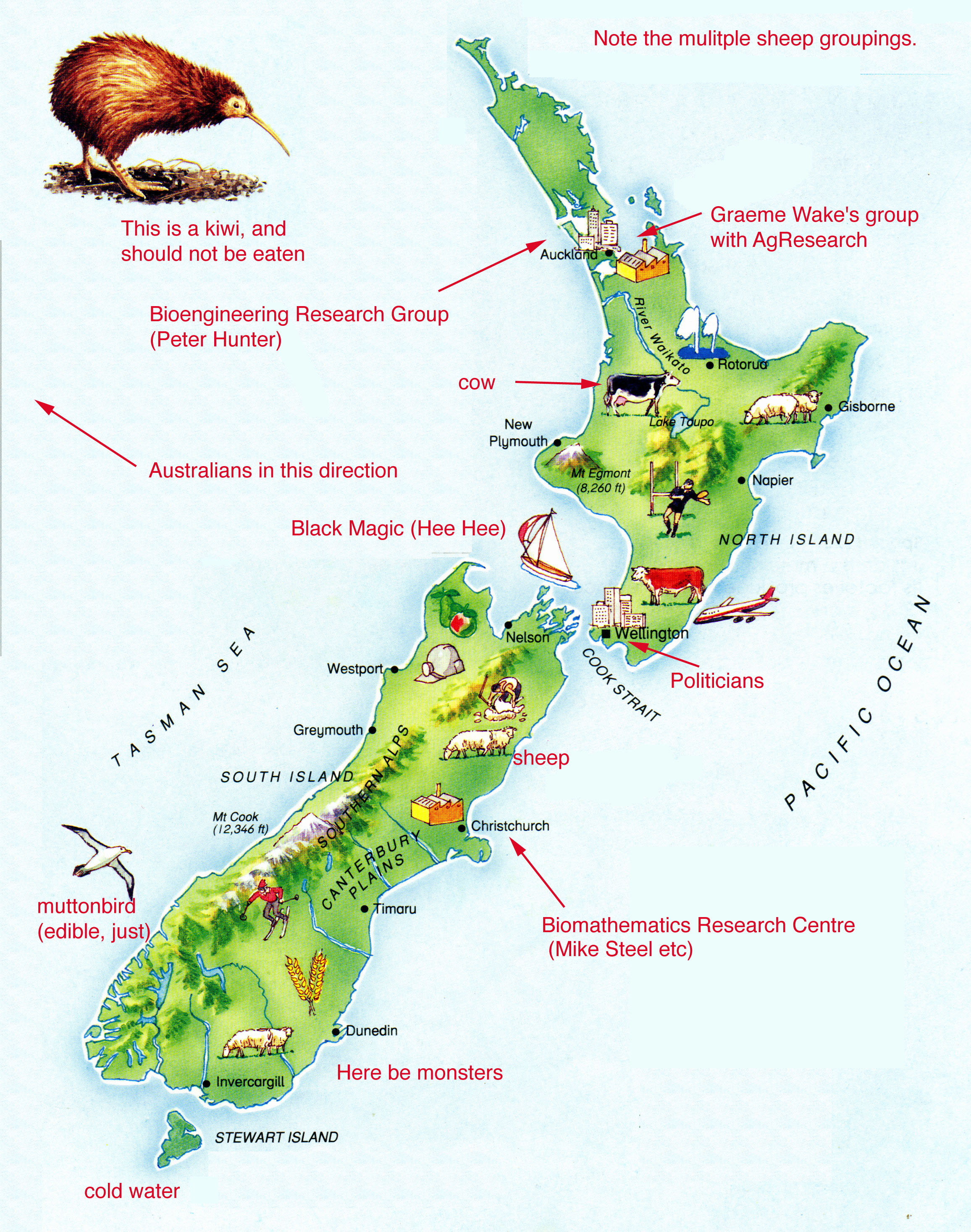
Since I am sure that many readers will have only a vague notion of what, or where, New Zealand is, let me begin with an introduction. Firstly, I state for the record that New Zealand is in fact a country. Not part of Australia, to which other country it happens to be physically close, a fact that causes considerable malicious confusion. It can be found about a thousand miles south-east of Australia, and consists of three major islands and a large number of smaller ones. The economy of New Zealand is based largely on sheep and cows, of which there are a very great many, and trees, of which there are also a great many, but they are counted less frequently. With a land area approximately that of Great Britain, and a population of somewhere between 3 and 4 million people, life there is uncrowded. Probably the most attractive aspect of the country, apart from the scenery, is that nobody knows who O.J. Simpson is. The principal religion is rugby.

Because the economy is so closely tied to primary production there is tremendous interest in, and support for, the study of ecological systems and the biology of populations. These topics are the principal focus of one of the major groups in mathematical biology in New Zealand, the University of Auckland and AgResearch Mathematical Biology Research Unit, headed by Graeme Wake ( http://www.math.auckland.ac.nz/~wake ). This group consists of a number of faculty members of the University of Auckland working closely alongside scientists in an Agricultural Research facility. Two present PhDs are working on Hill-land sustainability, earthworm activity and soil sulphur dynamics, while projects in the recent past have included animal growth processes, a stochastic model for ecological competition, cell-growth models in plants, and models for possum populations.

This last topic, the study of possums (and don't ask me what their Latin name is, I wouldn't have a clue), is an area in which many groups have worked, as the problem is central to the New Zealand economy and environment. Possums were introduced to New Zealand in the middle of last century, and, in the absence of significant predation, have expanded until now they can be found in almost every part of New Zealand. Not only do they destroy the native vegetation almost as efficiently as people do, they also are the principal resevoir of bovine tuberculosis. Since it is best to know thine enemy, a great deal of effort has been put into determining possum behaviour, and the best ways to kill them. (Interestingly, much the same thing can be said of rabbits, as the only good bunny is a dead one, but I know of much less modelling work done on rabbit populations in New Zealand.) As well as the work done by Graeme Wake's group, other principal players in the quantitative study of possum are Nigel Barlow and Murray Efford. Efford's model has made a particular effort to incorporate detailed spatial information for specific regions, and is one of the few models of this type I have seen. For instance, if possums need to be controlled in a specific region, then how should the kill be best distributed for maximum effect? A model can be a useful tool for answering this question.

Some of Efford's later work was done in collaboration with the Biomathematics Research Centre (BRC) at Canterbury University, another of the major research groups ( http://www.canterbury.ac.nz/maths/biomath.html). The BRC was established in 1996 and is directed by Mike Steel and David Wall. It has research efforts in a number of fields in addition to the work on possums described above. Principally, Mike Steel is an internationally recognised researcher in the field of evolutionary genetics. His collaboration with Mike Hendy and Dave Penny, both of Massey University, is now of some years standing, and has resulted in major advances in algorithms for the reconstruction of evolutionary trees. As an application of the theory, the group has studied the origin of native New Zealand fauna such as the kiwi and the moa. The kiwi, let me add, is a small brown flightless bird, not a small brown fuzzy fruit, which is actually called a kiwifruit. A trivial point you might think, and you would be right, but I still find it odd to hear people talking about eating kiwis. Moas are large brown flightless birds, now long extinct.

Another major research program at the BRC studies the physiology of neuroendocrine cells, and is led by Andrew LeBeau, David Wall, Bruce Robson, and Alan McKinnon. Its goal is to understand the mechanisms controlling the secretion of adrenocorticotropic hormone (ACTH) from anterior pituitary corticotrophs, and is presently focusing on the cellular mechanisms of ACTH release. One major stimulus for this work was the wonderful experimental work of Cliff Irvine and Sue Alexander. They insert a cannula into the facial vein of a conscious horse, and then manipulate the cannula via a venous pathway unique to the horse such that the cannula ends in a position immediately below the pituitary. This allows the determination of pituitary hormone output with much greater accuracy than that obtained by sampling from the peripheral circulation. I am told this doesn't hurt the horse at all; if it did, one would be tempted to try the experiment on lawyers.

Probably the best known biomathematics research group in New Zealand is that of Peter Hunter, in the Engineering Sciences department of Auckland University ( http://www.esc.auckland.ac.nz/Groups/Bioengineering/). This group studies the biochemical, mechanical and electrical properties of the heart, and has an extensive web of collaborations with other researchers overseas, as well as with experimentalists within New Zealand. Their research projects are far too numerous to list here, but their major contribution is probably the construction of a three dimensional finite element model of the heart based on finite deformation elasticity theory. This model incorporates some of the most detailed measurements of cardiac fibre architecture yet taken, includes interactions between electrical and mechanical effects, and more recent versions have even included data on the coronary circulation and cardiac energetics. Many people around the world have been involved in this work, including Denis Noble, Sasha Panfilov, Jim Bassingthwaite, and Andrew McCulloch.

Although I have only been able to give the briefest description of biomathematial research in New Zealand, I hope it is clear that there are many possibilities there for the biomathematician, whether interested in population level models, or cellular electrophysiology. As elsewhere in the world, mathematical biology is one of the fastest growing areas of applied math, and will continue to be so for the forseeable future. Even in such a far-flung corner of the globe, progress cannot be denied.

Back to the SMB Newsletter